Chapter5 Applications

Some significant applications are demonstrated in this chapter.

5.1 How to insert an image (with visual markdown editor)

[![RakuPanda](images/RakuPanda.png "Panda avatar"){width="200"}](https://marcelorosales.github.io/Research_Notebook/r-methods-and-how-tos.html#how-to-discharge-git-commits-to-avoid-conflicts-special-circumstances.)

5.2 Example two

Hello world!!

5.3 Linear Regression with formula

#Linear regression plot full example
library(ggplot2)

# Dummy data frame
df <- data.frame(x = c(1:100))
df$y <- 2 + 3 * df$x + rnorm(100, sd = 40)

# Linear regression
lm(y ~ x, df)

## 
## Call:
## lm(formula = y ~ x, data = df)
## 
## Coefficients:
## (Intercept)            x  
##     -10.983        3.219

fit <- lm(y ~ x, df) # Gives Intercept and the slope only.
summary(fit) #Gives a detail summary or the regression.

## 
## Call:
## lm(formula = y ~ x, data = df)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -102.776  -30.375    4.671   30.506   90.219 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -10.9832     8.4117  -1.306    0.195    
## x             3.2190     0.1446  22.259   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 41.74 on 98 degrees of freedom
## Multiple R-squared:  0.8349, Adjusted R-squared:  0.8332 
## F-statistic: 495.5 on 1 and 98 DF,  p-value: < 2.2e-16

# y =  a + b*x. a= Intercept, b = Slope. 
# y = mx + b is the same as above where m = slope and b= intercept 

p <- ggplot(data = df, aes(x = x, y = y)) +
  geom_smooth(method = "lm", se=FALSE, color="red", formula = y ~ x) +
  geom_point()
p

# GET EQUATION AND R-SQUARED AS STRING
# SOURCE: https://groups.google.com/forum/#!topic/ggplot2/1TgH-kG5XMA

lm_eqn <- function(df){
  m <- lm(y ~ x, df);
  eq <- substitute(italic(y) == a + b %.% italic(x)*","~~italic(r)^2~"="~r2, 
                   list(a = format(unname(coef(m)[1]), digits = 3),
                        b = format(unname(coef(m)[2]), digits = 3),
                        r2 = format(summary(m)$r.squared, digits = 3)))
  as.character(as.expression(eq));
}

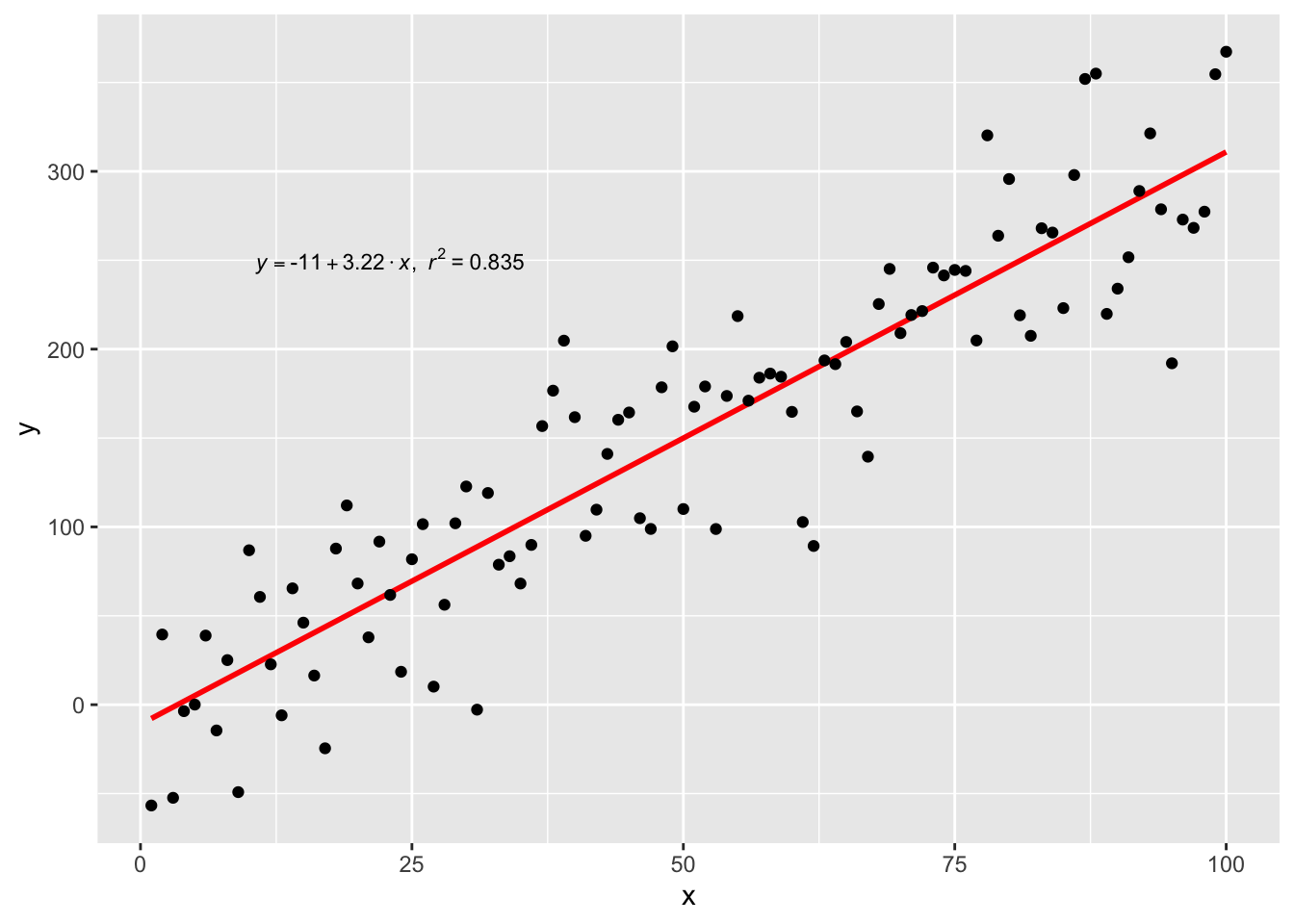
p1 <- p + geom_text(x = 25, y = 300, label = lm_eqn(df), parse = TRUE)
p1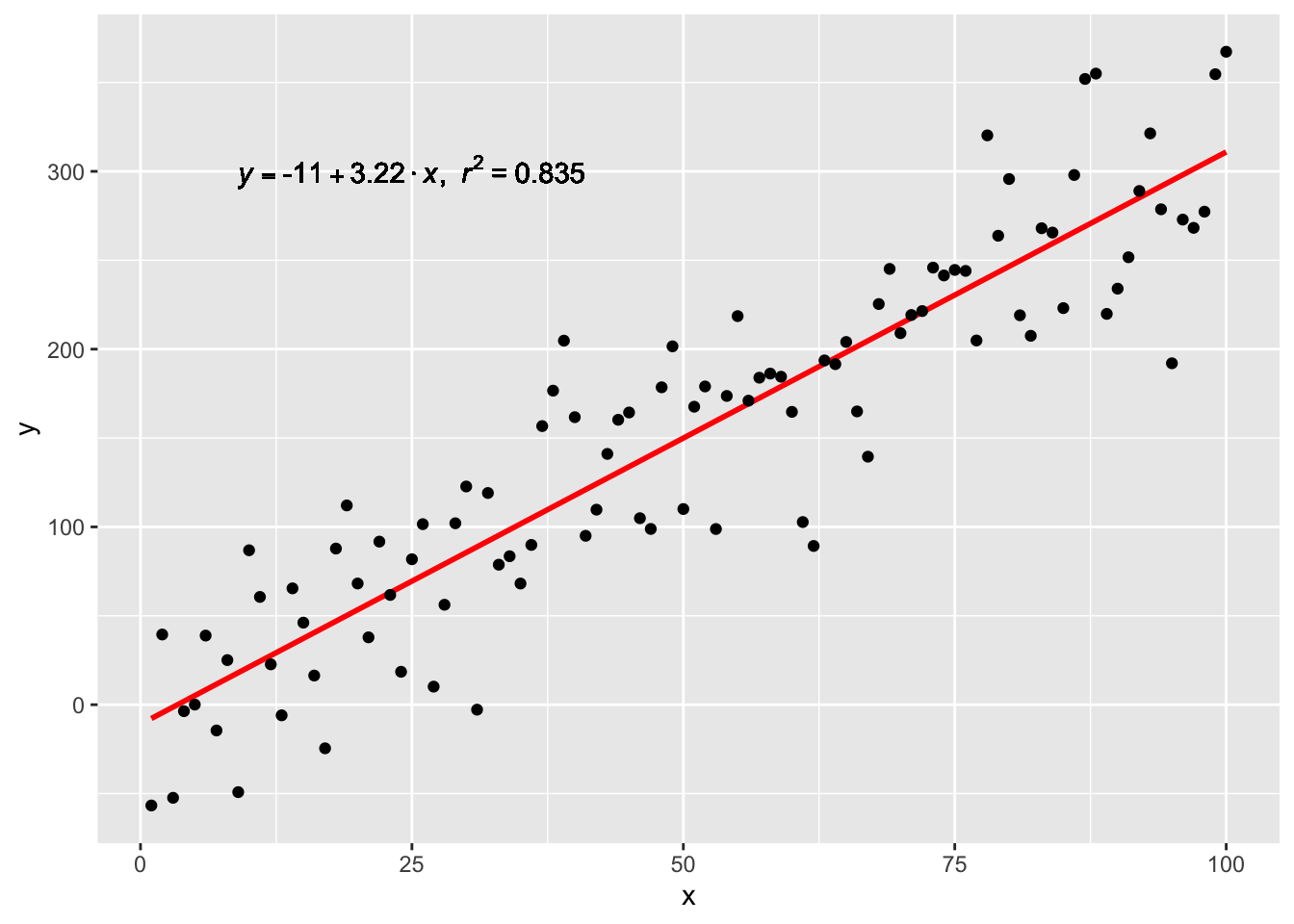

p2 <- p + annotate("text", x=23, y = 250, label = lm_eqn(df), color = "black", size = 3, parse=T)
p2